สมการแบร์นูลลี

พิจารราของไหลในท่อตามรูป เริ่มจากของไกลในท่อแนวระดับซ้ายมือซึ่งมีพื้นที่หน้าตัดสม่ำเสมอ a1 สูงจากระดับอ้างอิง h1 ไหลในเวลา t เป็นระยะทาง
 ของไหลส่วนนี้จะทำให้เกิดการไหลต่อเนื่องกันไปถึงท่อใหญ่แนวระดับขวามือที่มีพื้นที่หน้าตัดเนื่องกันไปถึงท่อใหญ่แนวระดับขวามือที่มีพื้นที่หน้าตัดสม่ำเสมอ A2 สูงจากระดับอ้างอิง h2 เมื่อการไหลในเวลา t เดียวกัน ได้ระยาทาง
ของไหลส่วนนี้จะทำให้เกิดการไหลต่อเนื่องกันไปถึงท่อใหญ่แนวระดับขวามือที่มีพื้นที่หน้าตัดเนื่องกันไปถึงท่อใหญ่แนวระดับขวามือที่มีพื้นที่หน้าตัดสม่ำเสมอ A2 สูงจากระดับอ้างอิง h2 เมื่อการไหลในเวลา t เดียวกัน ได้ระยาทาง  โดยมวลของไหลที่ผ่านทพื้นที่ทั้งสองมีค่าเท่ากันเท่ากับ
โดยมวลของไหลที่ผ่านทพื้นที่ทั้งสองมีค่าเท่ากันเท่ากับ ให้ทุกๆจุดในของไหลในท่อซ้ายือมีความดัน P1 อัตราเร็วเป็น v1 จะได้งานที่ทำโดยแรงดันในของไหลกระทำต่อของไหล

ให้ทุกๆตุดในของไหลในท่อขวามือมีความดัน P2 อัตราเร็วเป็น v2 จะได้ทำโดยแรงดันในของไหลกระทำต่อของไหล
จากความรู้เรื่องงานและพลังงาน เราทราบว่า งานที่ทำโดยแรงลัพธ์กระทำต่อระบบจะเท่ากับพลังงานจลน์ของระบบที่เปลี่ยนไป ในที่นี้ของไหลที่พิจารณาก็คือ ระบบ ดังนั้น

 เป็นปริมาตรของของไหลในท่อทั้งสองที่พิจารณาซึ่งของไหลจะมีมวล m เท่ากัน และความหนาแน่น
เป็นปริมาตรของของไหลในท่อทั้งสองที่พิจารณาซึ่งของไหลจะมีมวล m เท่ากัน และความหนาแน่น 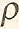
ดังนั้น

จะได้

สมการข้างต้นสรุปได้ว่า ผลรวมของความดันพลังงานจลน์ต่อหนึ่งหน่วยปริมาตร และพัลงงานศักย์ต่อหนึ่งหน่วยปริมาตร ณ จุด ใดๆ ภายในท่อที่มีของไหลผ่านมีค่าคงตัว ข้อสรุปดังกล่าวนี้เสนอโดยแบร์นูลลี และสมการแสดงความสัมพันธ์ดังกล่าวเรียกว่า สมการของแบร์นูลลี (Bernoulli's equation) ซึ่งเขียนได้เป็น



